연습문제 4.16

$ \def\mybar{\mskip1mu\vert\mskip1mu} $ 아들-딸 역설 : 두 자녀를 둔 가정에 딸이 적어도 한 명 있을 때 두 자녀 모두가 딸일 확률은 얼마인가? "딸이 적어도 한 명 있을 때"를 "첫째 아이가 딸일 때"로 바꾸면 어떻게 되는가?
(힌트). 표본공간 ${}= S=\{BB, BG, GB, GG\}$
딸이 적어도 1명 있는 사건 ${}= E_1 = \{BG, GB, GG\}$
두 자녀가 모두 딸인 사건 ${}=E_2 = \{GG\}$
첫 째 아이가 딸인 사건 ${}=E_3 = \{ GB, GG \}$
$P(E_2 \mybar E_1) = \frac{1/4}{3/4} = \frac{1}{3}$
$P(E_2 \mybar E_3) = \frac{1}{2}$
상자 속의 금화/은화: 세 상자 A, B, C 중 어느 하나에는 금화가 두 개 들어 있고, 다른 하나에는 금화와 은화가 하나씩, 그리고 나머지 하나에는 은화가 두 개 들어 있다. 상자를 하나 택하고 하나의 주화를 꺼내어 금화가 나온 경우, 그 상자에 남아 있는 또 하나의 주화가 금화일 확률은 얼마일까?
(힌트). $A = \{G_1, G_2\}$, $B = \{ G_3, S_1\}$, $C = \{S_2, S_3\}$로 두면 표본공간은 $S = \{G_1G_2, G_2G_1, G_3S_1, S_1G_2, S_2S_3, S_3S_2\}$가 된다.
첫 번째 주화가 금화인 사건 ${}= E_1 = \{ G_1G_2, G_2G_1, G_3S_1 \}$
두 번째 주화가 금화인 사건 ${} = E_2 = \{ G_1G_2, G_2G_1, S_1G_2\}$
상자 속의 금화/은화 #2: 위의 문제에서 $A = \{G_1, G_2, S_4\}$로 바꾸고, "상자에 남아 있는 또 하나의 주화가 금화일 확률"을 "그 상자에서 또 하나의 주화를 꺼내었을 때 그것이 금화일 확률"을 구하는 것으로 바꿔 보자.
(힌트). 이 경우 $S = \{\}$가 되는데 여기서 주의할 점은 근원사건들의 확률이 일정하지 않다는 것이다. 각 상자를 선택할 확률이 $\frac{1}{3}$로 동일하고, 상자 내에서 각 주화를 꺼낼 확률이 동일하다는 가정하에 다음과 같이 답을 구할 수 있다.

$S = \{G_1G_2, G_1S_4, G_2G_1, G_2S_4, S_4G_1, S_4G_2, G_3S_1, S_1G_2, S_2S_3, S_3S_2 \}$.

단 여기서 근원사건들의 확률은 다음과 같다:

$P(\{G_1G_2\}) = \cdots = P(\{S_4G_2\}) = \frac{1}{18}$,
$P(\{G_3S_1\}) = \cdots = P(\{S_3S_2\}) = \frac{1}{6}$

이제 다음과 같이 계산한다.
$E_1 = \{G_1G_2, G_1S_4, G_2G_1, G_2S_4, G_3S_1 \}$
$E_2 = \{ G_1G_2, G_2G_1, S_4G_1, S_4G_2, S_1G_2 \}$
$ P(E_2 \mybar E_1) = \frac{2/18}{4/18 + 1/6} = \frac{2}{7} $
몬티 홀 문제: 진행자가 관객들 앞의 무대에서 쇼를 진행한다. 무대에 3개의 닫혀진 문이 있다. 그 중 하나의 문 뒤에는 스포츠카가 있고 나머지 2개의 문 뒤에는 염소가 들어있다. 진행자는 관객 중에 행운의 1명(게스트라고 부르기로 라바)을 무대로 불러내어 문 뒤에 있는 것을 가져갈 권리를 준다. 게스트가 하나의 문을 선택한다. 아직 문을 열지 않은 상태에서 진행자는(어느 문 뒤에 스포츠카가 있는지 알고 있다) 염소가 들어있는 문을 열어 보여 준다. 그리고 무대 위에서 긴장하고 있는 게스트에게 현재 선택한 문이 아닌 다른 문을 열 수 있다고 말한다. 이때 게스트는 스포츠카를 갖기 위해 문을 바꾸는 것이 유리할까? 아니면 그대로 있는 것이 유리할까? 아니면 바꾸거나 말거나 스포츠카가 들어있는 문을 열게 될 확률에는 변화가 없을까?
인터넷에서 검색하면 이 문제의 풀이와 답을 알 수 있다. 그런데 거의 모든 해법에서 사건들을 집합으로 표현하지 않고, 즉 집합의 원소를 나열하지 않고 그냥 직관적으로 설명한다. 집합을 사용하여 설명해 보라.

이번에는 게임의 규칙을 바꾸어, 진행자가 자동차가 들어있는 방을 모르고 있어서 무작위로 문을 연 방에 스포츠카가 없었다고 가정하고 분석해 보라.

(힌트). 일반성의 손실 없이 스포츠카가 3번 문 뒤에 있다고 가정하기로 한다.

이해를 돕기 위해서 먼저 진행자가 개입하지 않는 단순한 경우를 분석해 보자. 이 경우의 표본공간은 오른쪽 그림과 같이 9개의 원소로 이루어져 있고 각 근원사건의 확률은 $\frac{1}{9}$이다. 이 그림에서 예를 들어 21은 게스트가 두 번째 문을 선택했다가 첫 번째 문으로 바꾼 것을 의미한다. 녹색 직사각형은 당첨되는 사건을 뜻하고 동그라미들은 문의 선택을 바꾸지 않는 사건을 나타낸다. 그러므로 문의 선택을 바꾸지 않았을 때의 당첨 확률은 $\frac{P(\{33\})}{P(\{11, 22, 33\})} = \frac{1}{3}$이 되고, 문의 선택을 바꾸었을 때의 당첨확률은 $\frac{P(\{13, 23\})}{P(\{12, 13, 21, 23, 31, 32\})} = \frac{1}{3}$로 동일한 값이 된다.

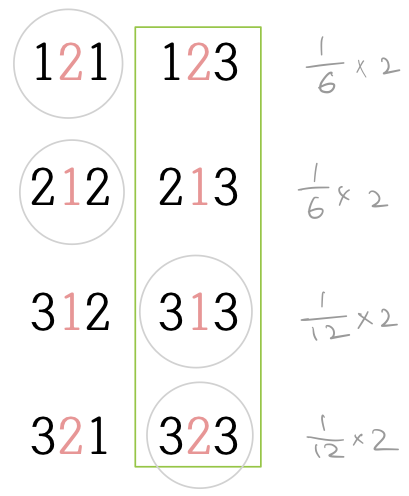이제 진행자가 개입하는 경우의 표본공간을 그려 보자. 붉은 색 숫자는 진행자가 열어 보인 문의 번호를 뜻한다. 게스트가 1번 문을 선택했다면 진행자는 2번 문을 열 수밖에 없고, 게스트가 2번 문을 선택했다면 진행자는 1번 문을 열어야 한다. 게스트가 3번 문을 선택했을 때는 진행자가 1번, 혹은 2번 문에서 하나를 열게 된다.

이 표본공간에서 근원사건들의 확률은 일정하지 않다. 예를 들어 근원사건 123의 확률은 처음에 게스트가 1을 선택할 확률 1/3에 문을 바꾸지 않을 확률 1/2을 곱하여 1/6이 된다. 근원사건 312의 경우는 게스트가 3을 선택하는 확률은 1/3으로 이전과 같지만 진행자가 1번 또는 2번 문을 열 확률이 각각 1/2이므로 이 두 확률의 곱에 최종적으로 게스트가 문을 바꿀(혹은 바꾸지 않을) 확률 1/2를 곱하면 1/12의 확률을 갖게 된다.

게스트가 문을 바꾸지 않았을 때의 당첨확률은 아래의 \eqref{eq:monty1}에, 바꾸었을 때의 당첨확률은 아래의 \eqref{eq:monty2}에 계산하였다.
\begin{gather} P(\{313, 323\}\mybar\{121, 212, 313, 323\}) = \frac{1/12 + 1/12}{1/6 + 1/6 + 1/12 + 1/12} = \frac{1}{3} \tag{$*1$}\label{eq:monty1} \\ P(\{123, 213\}\mybar\{123, 213, 312, 321\}) = \frac{1/6 + 1/6}{1/6 + 1/6 + 1/12 + 1/12} = \frac{2}{3} \tag{$*2$}\label{eq:monty2} \end{gather}
이번에는 게임의 규칙을 바꾸어 진행자가 자동차가 들어있는 방을 모르고 무작위로 문을 선택하여 열었을 때 스포츠카가 없었다고 하자. 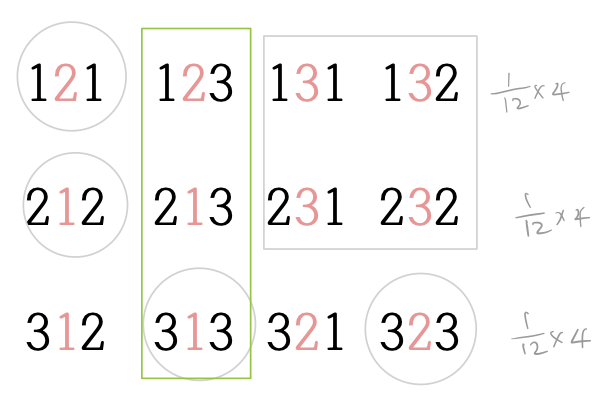이 경우의 표본공간은 오른쪽 그림과 같다. 131, 132, 231, 232의 4 경우는 발생할 수도 있었으므로 확률을 각각 1/12씩 부여 받는다. 이들을 회색 4각형으로 표시했으며 이 사건이 발생하지 않았다는 조건 하에 확률을 구해야 한다.

진행자가 문을 열기 전에는 게스트가 처음에 선택한 문 뒤에 스포츠카가 있을 확률은 1/3이다. 그러나 진행자가 문을 엶으로 해서 2번 방에는 스포츠카가 없다는 새로운 정보를 얻게 되었으므로 게스트가 처음에 선택한 문 뒤에 스포츠카가 있을 확률은 1/2로 증가한다.

원래의 문제에서는 게스트가 처음에 선택하지 않은 2개의 문 중 어느 하나의 뒤에 스포츠가가 있을 확률이 2/3이었는데, 답을 알고 있는 진행자가 2개의 문 중 하나를 열어 스포츠카가 없음을 보여주었으므로 제3의 문 뒤에 스포츠카가 있을 확률은 1/3에서 2/3로 증가한다. 그러나 처음에 게스트가 선택한 문 뒤에 스포츠카가 있을 확률은 진행자가 연 문 뒤에 스포츠카가 없었다는 새로운 정보에 의하여 변하지 않는다.

게스트가 문을 바꾸지 않았을 때의 당첨확률은 아래의 \eqref{eq:monty3}에, 바꾸었을 때의 당첨확률은 아래의 \eqref{eq:monty4}에 계산하였다.
\begin{gather} P(\{313, 323\}\mybar\{121, 212, 313, 323\}) = \frac{1/12 + 1/12}{1/12 + 1/12 + 1/12 + 1/12} = \frac{1}{2} \tag{$*3$}\label{eq:monty3} \\ P(\{123, 213\}\mybar\{123, 213, 312, 321\}) = \frac{1/12 + 1/12}{1/12 + 1/12 + 1/12 + 1/12} = \frac{1}{2} \tag{$*4$}\label{eq:monty4} \end{gather}

[홈으로]