\( \def\defeql{\stackrel{\mathrm{def}}{=}} \def\rR{\mathbb R} \newcommand{\nN}{\mathbb N} \def\st{\bigm\vert} \)범주형 자료{categorical data}란 관측값들을 몇 개의 속성에 의하여 범주로 분류하여 각 범주의 도수(자료의 수)를 표현하는 자료를 뜻한다. 범주형 자료는 양적자료가 아니므로 평균이나 분산을 계산할 수 없다. 따라서 지금까지 공부했던 여러 통계 분석 기법들은 범주형 자료에 적용하기 곤란한 경우가 대부분이다.
범주형 자료의 분석 중 가장 널리 쓰이는 3개의 방법을 알아보고자 한다.
(1. 적합도 검정). 모집단의 각 범주에 속하는 빈도의 이론적 비율이, 표본의 각 범주에 속하는 관측빈도로부터 계산하여 얻은 비율과 일치하는지를 평가하는 것을 적합도 검정(goodness of fit test)이라 한다.

적합도 검정의 귀무가설은 "각 범주의 관측확률 $\frac{o_i}{n} \defeql p_{oi}$가 기대확률 $p_i$와 일치한다."로 잡는다. 즉, \begin{equation*} H_0: p_i = p_{oi}\;(i=1,\ldots,k),\quad H_1: \text{not } H_0 \end{equation*} 로 둔다. 검정통계량은 \[ \chi^2 = \sum_{i=1}^k \frac{(O_i-E_i)^2}{E_i} \sim \chi^2(k-1) \] 이다. 이 분석법은 $E_i \ge 5$인 경우에만 사용할 수 있다.
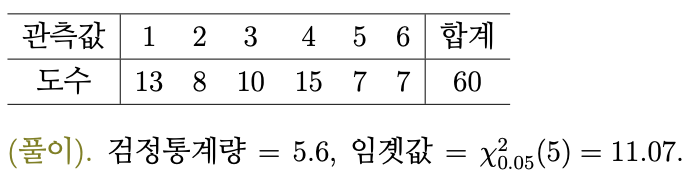
(연습문제). 주사위를 60회 던져서 아래의 표와 같은 결과를 얻었다. 이 주사위가 공정한 것인지를 유의수준 5%에서 검정하여라.
(2. 독립성 검정). 질적자료를 2개의 속성에 따라 범주로 나누었을 때 이 속성들이 (관찰값에 미치는 영향이) 서로 독립적인지 아닌지를 판별하는 것을 독립성 검정(test of independence)이라 한다. 독립성 검정의 자료는 통상 아래와 같은 분할표(contingency table)로 나타낸다.
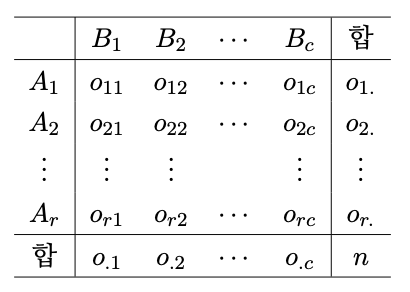
위의 표에서 속성 $A$와 속성 $B$가 서로 독립인지를 판별하는 검정통계량은 아래와 같다. \begin{equation}\label{eq:indep_stat} \chi^2 = \sum_{i=1}^r\sum_{j=1}^c \frac{(O_{ij}-\hat E_{ij})^2}{\hat E_{ij}} \sim \chi^2\bigl((r-1)(c-1)\bigr) \end{equation} 단, \begin{align*} \hat e_{ij} &= n \times \hat p_{ij} \\ \hat p_{ij} &= \hat p_{i.}\times \hat p_{.j} \\ \hat p_{i.} &= \frac{o_{i.}}{n},\; \hat p_{.j} = \frac{o_{.j}}{n} \end{align*} 검정할 가설은 \begin{equation}\label{eq:indep_hyp} H _0: p_{ij} = p_{i.}\times p_{.j},\;(\forall i,j),\quad H_1: \text{not } H_0 \end{equation}
독립성 검정의 가설은 \eqref{eq:indep_hyp}\와 같이 써도 좋지만 아래와 같이 쓰는 것이 일반적이다. \begin{equation*} H _0: \text{속성 $A$와 $B$는 독립이다},\quad H_1: \text{not } H_0 \end{equation*}
(예제). 아래의 분할표에 주어진 자료를 유의수준 5%에서 독립성 검정을 해 보자.
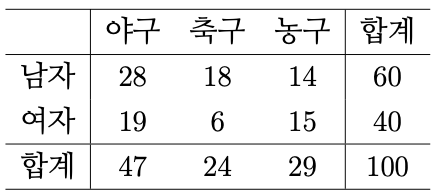
(풀이)
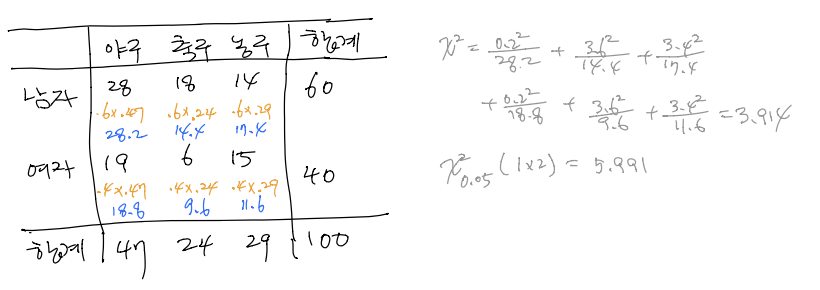
(3. 동질성 검정). 이 검정에서 사용하는 자료구조는 다음과 같다. $B_1,\ldots,B_c$는 속성이고 $A_1,\ldots,A_r$은 부분모집단이다.
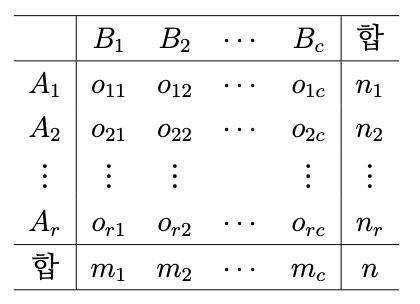
위의 표는 독립성 검정의 표와 사실상 동일하다. 다만 행과 열의 합을 나타내는 기호만 다를 뿐이다.
동질성 검정은 부분모집단들이 속성 $B_j (j=1,\ldots,c)$에 대하여 동질(homogeneous)인지를 검정하는 것이다. 즉, \begin{equation} H_0: \frac{O_{1j}}{n_1} = \cdots = \frac{O_{rj}}{n_r},\; (j=1,\ldots,c),\quad H_1: \text{not } H_0 \label{h0_homo} \end{equation} 이 검정은 실질적으로 독립성 검정과 같다. 다만 관점의 차이가 있을 뿐이다. 검정통계량은 \eqref{eq:indep_stat}를 그대로 쓰면 된다.
동질성 검정이 독립성 검정과 사실상 같은 검정이라는 것을 증명해 보자. \begin{equation}\label{eq:indep_homo} (\forall j)\left(\frac{o_{1j}}{n_1} = \cdots = \frac{o_{rj}}{n_r}\right) \Leftrightarrow (\forall i,j)\left(\frac{o_{ij}}{n} = \frac{n_i}{n}\times\frac{m_j}{n}\right) \end{equation}
(증명). $\Leftarrow$: \eqref{eq:indep_homo}의 우변을 가정하자. 그러면 \begin{align*} \frac{o_{ij}}{n_i} = \frac{o_{ij}}{n}\times\frac{n}{n_i} = \left(\frac{n_i}{n}\times\frac{m_j}{n}\right)\times\frac{n}{n_i} = \frac{m_j}{n} \end{align*} 이므로 $i$에 상관없이 (각 $j$에 대하여) 일정하다.
$\Rightarrow$: \eqref{eq:indep_homo}의 좌변을 가정하자. $j=1,\ldots,c$ 각각에 대하여 $\frac{o_{ij}}{n_i}$가 $i$에 무관하게 일정하므로 이를 $k_j := \frac{o_{ij}}{n_i}$로 두면 \begin{align*} \frac{o_{ij}}{n} = \frac{n_i}{n}\times k_j \end{align*} 이므로, $k_j = \frac{m_j}{n}$만 보이면 된다. 이제 \begin{align*} m_j = \sum_{i=1}^r o_{ij} = \sum_{i=1}^r (n_i \cdot k_j) = k_j\sum_{i=1}^r n_i = k_j\cdot n \end{align*} 이므로 원하던 $k_j = \frac{m_j}{n}$를 얻게 된다. $\quad\Box$
(연습문제). 어느 담배 제조회사에서 30세 이상의 성인 남자를 대상으로 흡연율을 조사한 결과 아래의 표를 얻었다. 유의수준 5%에서 각 연령층별로 흡연율에 차이가 있는지를 검정하시오.
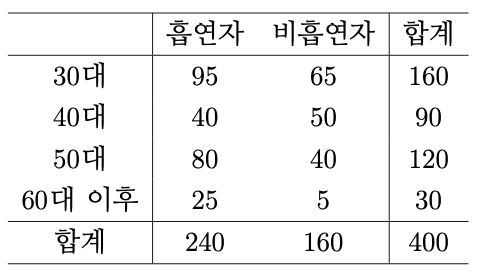
답(의 일부) : 검정통계량 = 18.12, 임곗값 = $\chi^2_{0.05}(3) = 7.81$
[홈으로]