서로 독립이 아닌 두 모집단에 대한 표본의 대표적인 예로 짝지어진 표본(paired sample)이 있다.
예를 들어 어떤 운동 프로그램이 학생들의 체중을 줄이는 데 얼마나 효과가 있는지 알아보기 위하여 운동을 하지 않는 $n$명의 학생으로 표본을 구성하고, 운동을 하는 $m$명의 학생으로 또 하나의 표본을 구성하였다면, 이런 경우의 통계분석에는 앞서 공부한 방법을 적용하면 된다.
하지만 이보다는 $n$명의 학생을 뽑아 놓고 $i$번째 학생의 운동 전후의 체중을 각각 $x_i$, $y_i$로 기록하는 것이, 즉 표본 데이터를 $(x_1,y_1), \ldots, (x_n,y_n)$으로 짝지어지도록 하는 것이 좋다. 이때의 표본은
\begin{equation*} \{x_1-y_1, x_2-y_2, \ldots, x_n - y_n\} := \{d_1, d_2, \ldots, d_n \} \end{equation*}의 1개 뿐인 것으로 생각할 수 있다.
예를 들어 다음과 같은 자료가 주어졌을 때 이전의 방법으로 분석해 보면
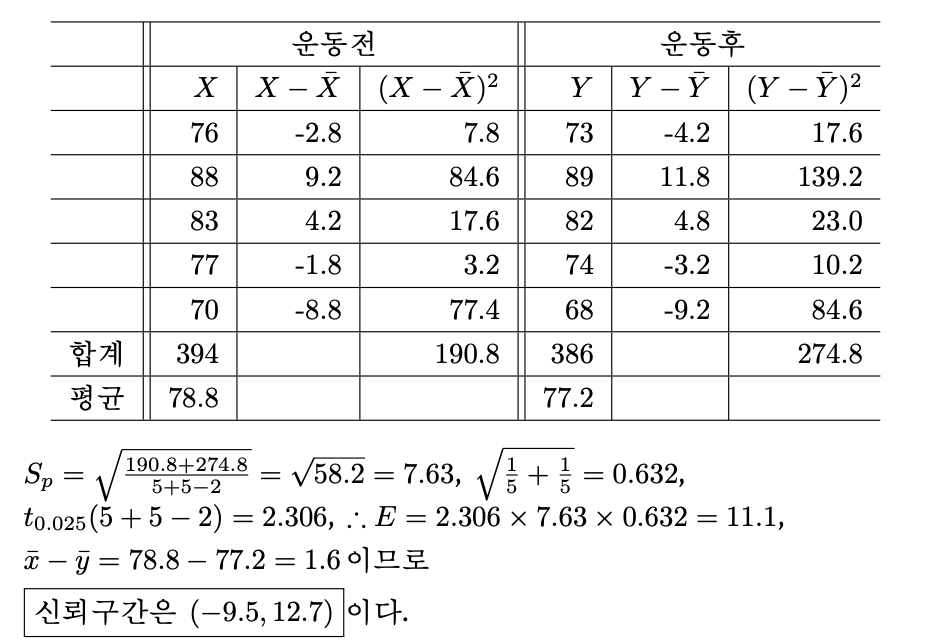
이번에는 두 표본이 독립적이 아니라 짝지어진 표본인 것으로 보고 계산해 보자.
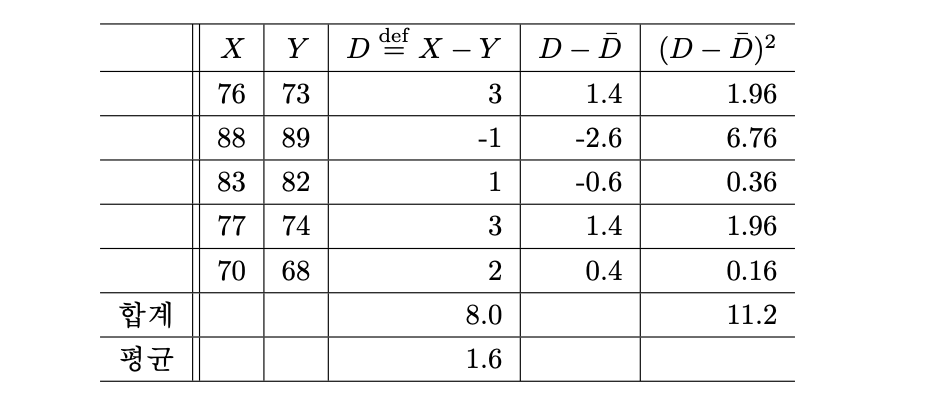

신뢰구간의 길이가 훨씬 더 작아졌음을 볼 수 있다.
[홈으로]