조건부 확률함수에서 그 조건이 $u(\vec X) = U$ 형태인 경우, 이 조건부 확률함수를 계산할 때 분모에 들어가는 주변확률함수 $f_U(u)$를 얻는 방법에 대하여 생각해 보자.
$D_u := \{\vec x\bigm\vert u(\vec x) = u \}$로 놓았을 때 \begin{equation}\label{eq:constrained_denom} f_U(u) = \begin{cases} \sum_{\vec x\in D_u} f(\vec x) &\text{discrete case}, \\[1.5ex] \int_{D_u} f(\vec x) \mskip2mu\mathrm{d}\vec x &\text{continuous case (wrong!)} \end{cases} \end{equation} 를 사용하면 될 듯 하다. 그러나 이 식 \eqref{eq:constrained_denom}은 이산형의 경우에는 맞으나 연속형인 경우에는 틀린다.
다음의 예에서 실제 계산을 통하여 위에서 설명한 내용을 이해하도록 하자.
$X \sim N(\mu, 1)$일 때 $\vec X = (X_1, X_2)$로 두면 $\vec X$의 결합확률함수는, $X_1$과 $X_2$가 서로 독립이므로 \begin{equation}\label{eq:joint_fn} f(\vec x) = f(x_1)\cdot f(x_2) = \left(\frac{1}{\sqrt{2\pi}}\right)^2 e^{-\frac{1}{2}\left((x_1 - \mu)^2 + (x_2-\mu)^2\right)} \end{equation} 로 주어지게 된다. ($f(\vec x)$는 원래는 $f_{\mathrm{joint}}(\vec x)$ 등으로 나타내어 1변수 함수 $f(x)$와 구별됨을 보여야 하지만 표기의 편의상 그냥 이렇게 쓴 것이다.)
이때 통계량 $U$를 $U = u(\vec X) := X_1 + X_2$로 정의하면 \begin{equation}\label{eq:f_Uu} f_U(u) = \frac{1}{2\sqrt{\pi}} e^{-\frac{1}{4}(u - 2\mu)^2} \end{equation} 임을 [예제 6.24]에서 보인 바 있다. 이 결과를 \eqref{eq:constrained_denom}을 사용하여 구해 보자.
이 문서에서 다음의 공식을 별도의 언급없이 수시로 사용할 것이다. \begin{equation}\label{eq:bell_int2} \int_{-\infty}^\infty e^{-(ax+b)^2} \,\mathrm{d}x = \frac{\sqrt{\pi}}{|a|} \end{equation}
$f_U(u)$는 일종의 주변확률함수이므로 이를 구하기에 앞서, 우리가 잘 아는 주변확률함수 $f_{X_2}(x_2)$의 식을 먼저 구해 보자. 이것의 해법은 단순히 $X_2 \sim N(\mu, 1)$이므로 $f_{X_2}(x_2) = \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}(x_2 - \mu)^2}$으로 두어도 되겠지만, 원칙대로 하면 주변확률함수의 정의에 따라서 \begin{align*}\label{eq:marginal_fn1} f_{X_2}(x_2) &= \int_{-\infty}^\infty f(x_1, x_2) \,\mathrm{d}x_1 = \int_{-\infty}^\infty \left(\frac{1}{\sqrt{2\pi}}\right)^2 e^{-\frac{1}{2}\left((x_1 - \mu)^2 + (x_2-\mu)^2\right)} \,\mathrm{d}x_1 \\[1.5ex] &= \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}(x_2 - \mu)^2} \times\int_{-\infty}^\infty \frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}(x_1 - \mu)^2} \,\mathrm{d}x_1 \\[1.5ex] &= \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}(x_2 - \mu)^2} \times 1 \end{align*} 로 계산하여 동일한 값을 얻을 수 있다.
한편 $\int_{-\infty}^\infty f(x_1, x_2) \,\mathrm{d}x_1 $은 적분의 정의에 의하여 $D = \{ \vec x \bigm\vert X_2 = x_2 \}$로 두고 \begin{equation*}\label{eq:def_fX2x2} \int_D f(\vec x)\, \mathrm{d}x_1\mathrm{d}x_2 \end{equation*} 를 계산한 값이다.
이제 $f_U(u)$를 구할 때는 \[ D = \{ \vec x \bigm\vert X_1 + X_2 = u \}\] 로 두고 \begin{equation}\label{eq:def_fUu} f_{U}(u) = \int_D f(\vec x)\; \mathrm{d}x_1\mathrm{d}x_2 \end{equation} 로 계산하면 될 것으로 보인다.
$D$는 직선이므로 다음과 같이 매개변수를 써서 나타낼 수 있다. \begin{align*} x_1 &= t \\ x_2 &= u - t \end{align*} 선적분(line integral)에 대한 경험이 적은 독자라면 $t=0$에서 출발하여 $t$의 값이 증가, 혹은 감소할 때 점 $(x_1, x_2)$가 직선 $x_1 + x_2 = u$를 따라 어떻게 이동하는지를 마음 속에 그려 보는 것이 도움될 것이다.
그러면 $\mathrm{d}s = \sqrt{1^2 + (-1)^2}\mskip2mu\mathrm{d}t = \sqrt 2\mskip2mu\mathrm{d}t$이므로 2중적분 \eqref{eq:def_fUu}는 \eqref{eq:joint_fn}에 있는 $f(\vec x)$의 식을 이용하여 다음의 선적분으로 변환된다. \begin{equation}\label{eq:to_integrate1} f_U(u) = \int_{-\infty}^\infty \frac{1}{2\pi} e^{-\frac{1}{2} \bigl( (t - \mu)^2 + (u-t-\mu)^2\bigr)} \,\sqrt 2\mskip2mu\mathrm{d}t \end{equation} 위 식의 $e$의 지수에서 $-\frac{1}{2}$를 떼어 놓고 보면 \begin{align*} (t-\mu)^2 + (u-t-\mu)^2 &= \bigl(t^2 + \mu^2 - 2t\mu\bigr) + \bigl( u^2 + t^2 + \mu^2 - 2ut + 2t\mu - 2u\mu\bigr) \\[1.5ex] &= 2t^2 -2tu + \frac{u^2}{2} + \frac{u^2}{2} -2u\mu + 2\mu^2 \\[1.5ex] &= 2\left(t-\frac{u}{2}\right)^2 + \frac{1}{2}(u - 2\mu)^2 \end{align*} 이 된다. 그러므로 \eqref{eq:to_integrate1}는 다음과 같이 계산된다. \begin{align} f_U(u) &= \int_{-\infty}^\infty \frac{1}{2\pi} e^{ -\frac{1}{2} \bigl( 2(t - u/2)^2 + (u - 2\mu)^2/2 \bigr) } \,\sqrt 2\mskip2mu\mathrm{d}t = \int_{-\infty}^\infty \frac{1}{\sqrt 2\pi} e^{ -(t - u/2)^2 } e^{- (u - 2\mu)^2/4 } \mskip2mu\mathrm{d}t \notag \\[1.5ex] &= \frac{1}{\sqrt 2\pi} e^{-\frac{1}{4} (u - 2\mu)^2 } \int_{-\infty}^\infty e^{ -(t - u/2)^2 } \mskip2mu\mathrm{d}t \label{eq:intersect_curve} \\[1.5ex] &= \frac{1}{\sqrt 2\pi} e^{-\frac{1}{4} (u - 2\mu)^2 } \sqrt \pi = \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{4}(u - 2\mu)^2} \label{eq:f_Uu2} \end{align} 이 결과는 \eqref{eq:f_Uu}과 거의 비슷하지만 $\sqrt 2$배 크게 나왔다!
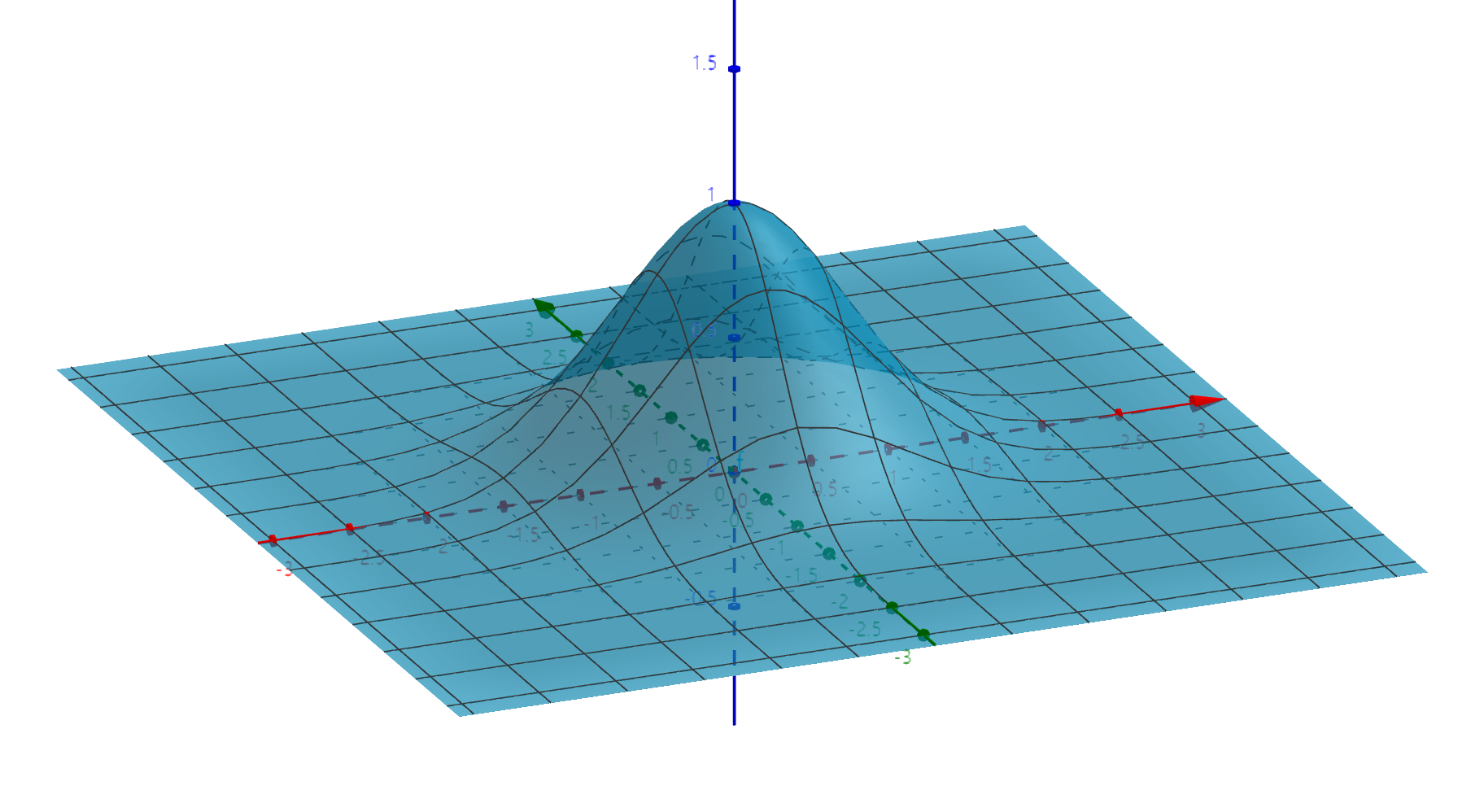
무엇이 잘못되었는지를 알아 내기 위하여 아래에 $z = f(\vec x)$의 그래프를 $\mu=0$인 경우에 대하여 그려보았다.

$u$를 어떤 실수라 하고 $x_1 x_2$평면상에 직선 $x_1 + x_2 = u$을 그린 다음, 이것을 품고 $z$축에 수직한 평면을 그려 보라.(마음 속에서) 이 평면과 그래프의 교선(교집합 곡선)의 식은 \eqref{eq:intersect_curve}에서 볼 수 있듯이 어떤 상수 $k$에 대하여 $z = ke^{ -(t - u/2)^2 }$이다.
이 적분을 시각적으로 파악하려면 $s = \sqrt 2 t$로 치환하여 곡선의 방정식을 $z = k'e^{ -(s/\sqrt 2 - u/2)^2 }$로 놓는 것이 더 좋겠다. 이렇게 하면 $s$는 점 $(x_1, x_2)$가 $(u,0)$에서 출발하여 이동하는 거리가 된다. (단, 이때의 거리에는 부호가 있다. $x_1$의 부호와 $s$의 부호는 일치한다.) 그리고 $(x_1, x_2, z)$의 궤적이 곧 교선을 이루며, 이것은 $s=u/\sqrt 2$에서 최댓값 $k'$을 가지는 종모양 곡선(bell-shaped curve)이 된다.
그래프와 $x_1 x_2$평면 사이의 입체의 부피는 확률밀도를 전체 영역에서 적분하여 얻은 값이므로 1이 된다. 이 입체와 평면 $x_1 + x_2 = u$의 단면적이 \eqref{eq:f_Uu2}에서 구한 $f_U(u)$이다.
이상의 논의는 상당히 그럴듯 하지만 결정적인 결함이 있다. $\int_{-\infty}^\infty f_U(u) \mskip2mu\mathrm{d}u = \sqrt 2 \ne 1$이 문제다. 이러한 문제가 발생하는 이유는 $\mathrm{d}V \neq f_U(u)\mathrm{d}u$이기 때문이다.
다변수 함수의 미분적분에 익숙하지 않은 독자라면 아래의 내용을 읽기 전에 책의 제3.3.4절 (적분을 미분하기)를 일독할 것을 권한다.
$f_U(u)$는 다음의 식을 만족하도록 정의되어야 한다. \begin{equation} \int_{-\infty}^w f_U(u) \,\mathrm{d}u = P[ U \le w] = P[ X_1 + X_2 \le w],\quad (\forall w\in\mathbb R) \end{equation} 그런데 $x_1 + x_2 \le w \Leftrightarrow x_1 \le w - x_2$이므로 \[ P[ X_1 + X_2 \le w] = \int_{-\infty}^\infty \int_{-\infty}^{w - x_2} f(x_1, x_2) \, \mathrm{d}x_1\mathrm{d}x_2 \] 이다. 따라서 \begin{align*} f_U(w) &= \frac{\mathrm{d}}{\mathrm{d}w} \int_{-\infty}^w f_U(u) \,\mathrm{d}u = \frac{\mathrm{d}}{\mathrm{d}w} \int_{-\infty}^w P[ X_1 + X_2 \le w] \,\mathrm{d}u \\[1.5ex] &= \frac{\mathrm{d}}{\mathrm{d}w} \int_{-\infty}^\infty \int_{-\infty}^{w - x_2} f(x_1, x_2) \, \mathrm{d}x_1\mathrm{d}x_2 \\[1.5ex] &= \int_{-\infty}^\infty \left( \frac{\partial}{\partial\,w} \int_{-\infty}^{w - x_2} f(x_1, x_2) \, \mathrm{d}x_1\right) \,\mathrm{d}x_2 \\[1.5ex] &= \int_{-\infty}^\infty f(w-x_2, x_2) \,\mathrm{d}x_2 = \int_{-\infty}^\infty \frac{1}{2\pi} e^{-\frac{1}{2} \bigl( (w-x_2-\mu)^2 + (x_2 - \mu)^2\Bigr)} \,\mathrm{d}x_2 \end{align*} 위 식의 마지막 항의 $e$의 지수에서 $-\frac{1}{2}$를 떼어 놓은 것에 \eqref{eq:to_integrate1}에서와 똑같은 기법을 사용하여 다음과 같이 계산을 이어갈 수 있다. 여기서 계산의 포인트는 두 곳에 있던 적분변수 $x_2$를 한 곳으로 모으는 데 있다. 또 하나 주목할 것은 \eqref{eq:to_integrate1}에서의 $\sqrt 2\mskip2mu\mathrm{d}t$가 여기서는 계수 $\sqrt 2$가 없는 $\mathrm{d}x_2$로 바뀌었다는 것이다. \begin{align*} f_U(w) &= \int_{-\infty}^\infty \frac{1}{2\pi} e^{-\frac{1}{2} \bigl( 2(x_2-w/2)^2 + (w - 2\mu)^2/2\Bigr)} \,\mathrm{d}x_2 \\[1.5ex] &= \frac{1}{2 \sqrt \pi} e^{-\frac{1}{4} (w - 2\mu)^2} \times \int_{-\infty}^\infty \frac{e^{-(x_2 - w/2)^2}}{\sqrt \pi}\,\mathrm{d}x_2 \\[1.5ex] &= \frac{1}{2 \sqrt \pi} e^{-\frac{1}{4} (w - 2\mu)^2} \times 1 \end{align*} 이제 $w$를 $u$로 치환하여 \eqref{eq:f_Uu}에서 보았던 $f_U(u)$의 올바른 값을 얻을 수 있다.
$\int_{-\infty}^\infty f_U(u)\,\mathrm{d}u = 1$이 됨은 쉽게 확인할 수 있을 것이다. $\quad\Box$
[홈으로]