함수 $f:\mathbb R \rightarrow \mathbb R$는 다음 조건을 만족할 때 구간 $(a,b)\subseteq\mathbb R$에서 위로 볼록이라고 한다. \begin{equation}\label{eq:def_convex} (\forall x_1 < x_2\in(a,b))(\forall t\in[0,1]) \Bigl( f\bigl(tx_1 + (1-t)x_2\bigr) > t f(x_1) + (1-t)f(x_2) \Bigr) \end{equation}
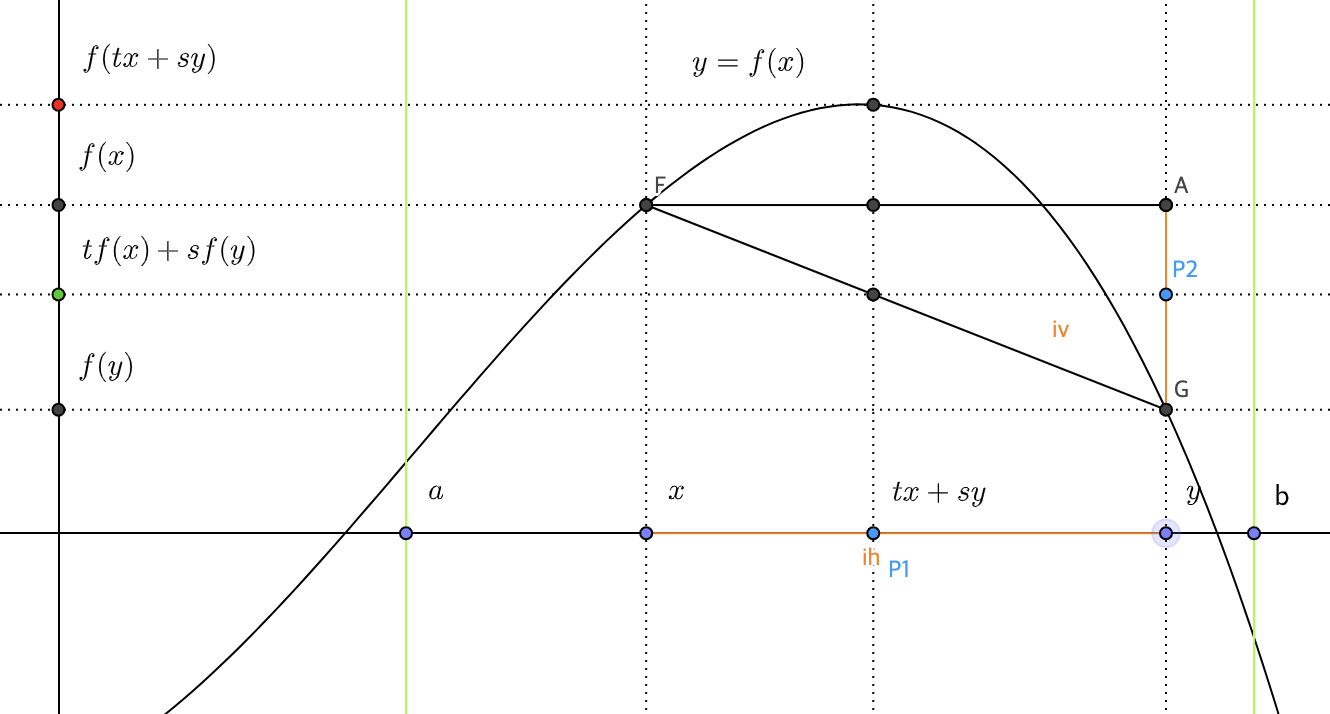
아래의 그림에서 $x=x_1$, $y=x_2$, $s=1-t$로 두고 보도록 한다. \eqref{eq:def_convex}의 부등식의 좌변은 $x$축 상의 선분 $\overline{xy}$의 $1-t:t$ 내분점에서의 $f$값이고, 우변은 선분 $\overline{FG}$, 즉 할선(secant)의 $1-t:t$ 내분점의 $y$좌표이다. 점 $P1$을 좌우로 움직일 때 $y$축 상의 빨간 점과 녹색 점의 움직임이 어떻게 되겠는지 마음 속에 그려 보라.
$f$의 2계 미분계수가 구간 $I:=(u,v)$에서 항상 존재한다면, (1) $(\forall x\in I)(f''(x) < 0)$는 $f$가 $I$에서 위로 볼록일 필요충분조건이 되고, (2) $(\forall x\in I)(f''(x) > 0)$는 $f$가 $I$에서 아래로 볼록일 필요충분조건이 된다.
이 정리의 증명은 다음의 따름정리 뒤에 보이겠다.
함수 $f:\mathbb R \rightarrow \mathbb R$가 구간 $I$에서 2계미분가능하다고 할 때 다음의 4 명제는 모두 서로 동등하다. 단, $m_1$, $m_2$, $m_3$는 아래의 그림에서 각각 선분 $\overline{AB}$, $\overline{BC}$, $\overline{AC}$의 기울기이다. 즉, \[ \begin{split} m_1 &= \frac{f(b)-f(a)}{b-a} \\[1.5ex] m_2 &= \frac{f(c)-f(b)}{c-b} \\[1.5ex] m_3 &= \frac{f(c)-f(a)}{c-a} \end{split} \]
① : $f$는 구간 $I$에서 아래로 불록이다.
② : $(\forall a < b < c \in I)(m_1 < m_2)$
③ : $(\forall a < b < c \in I)(m_1 < m_3)$
④ : $(\forall a < b < c \in I)(m_3 < m_2)$
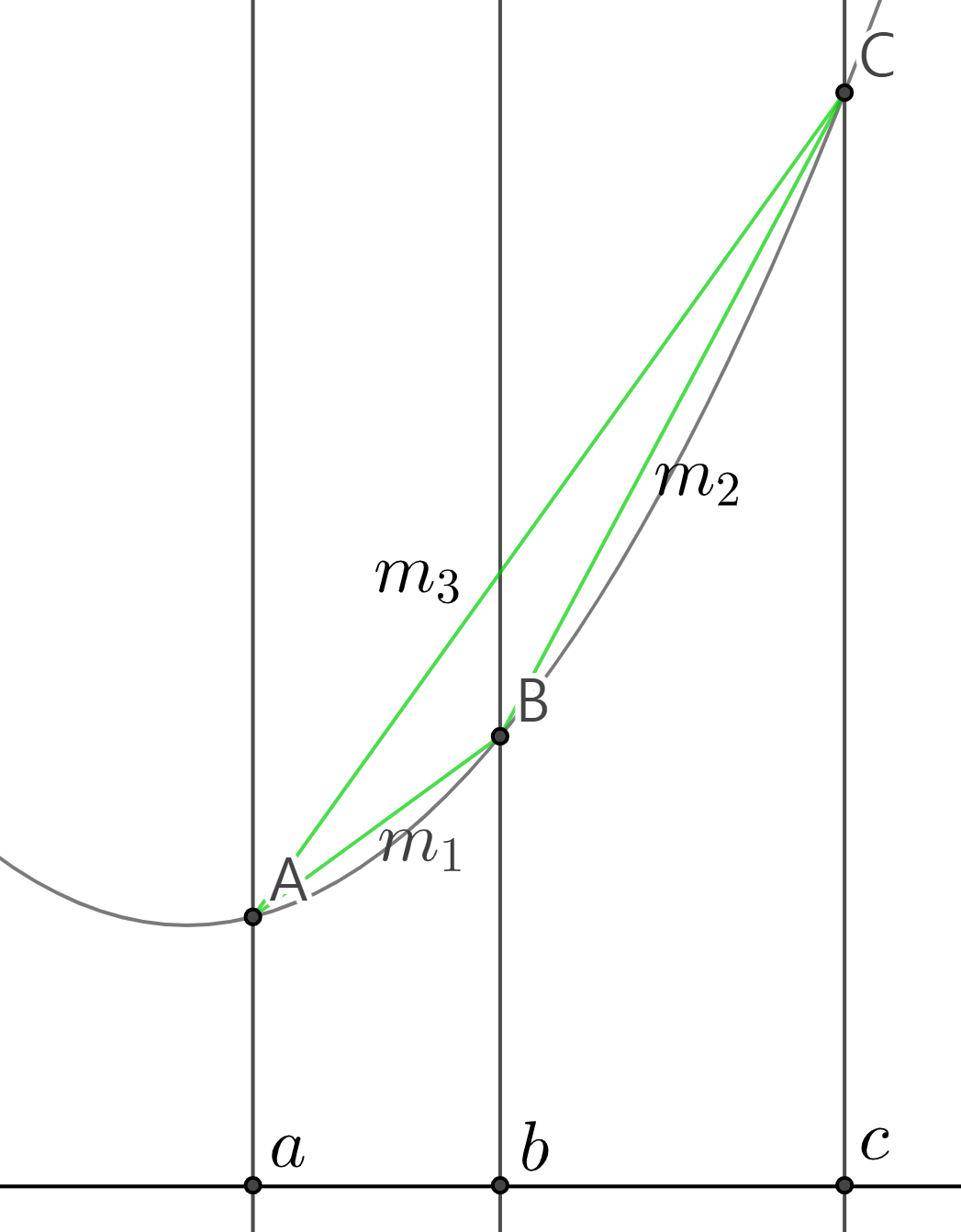
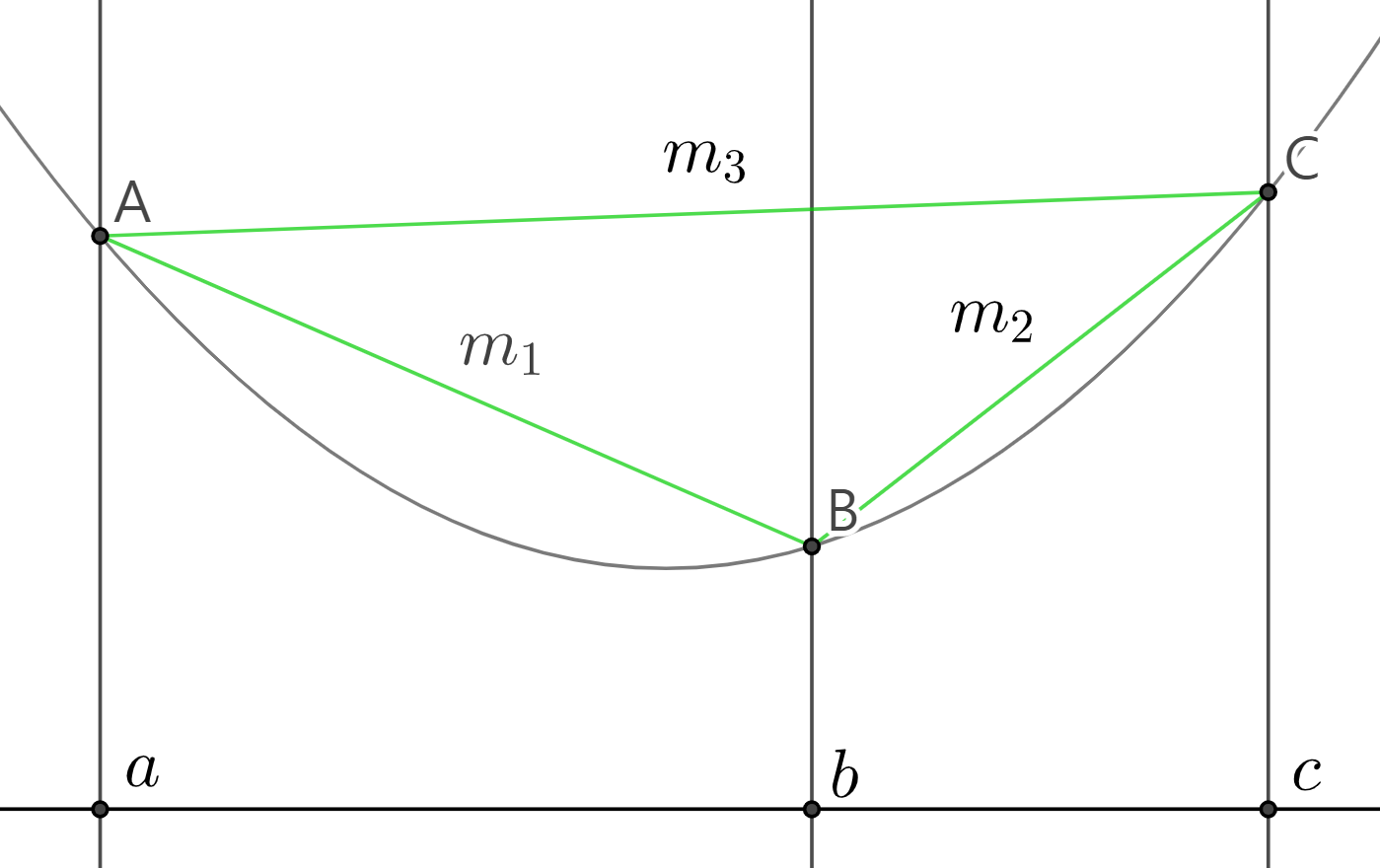
(증명). $t = \frac{b-a}{c-a}$로 두면 $1-t = \frac{c-b}{c-a}$이고 $b = (1-t)a + tc$이다. 이 사실은 그림으로부터 알 수 있으며 계산으로도 쉽게 확인 가능하다.
$f$가 구간 $I$에서 아래로 볼록이면 모든 $a < b < c \in I$에 대하여 다음의 식들이 성립하며 이들은 모두 서로 등동하다. \begin{align*} f((1-t)a & + tc) < (1-t)f(a) + tf(c) \\[1.5ex] &\Leftrightarrow f(b) < \frac{c-b}{c-a}f(a) + \frac{b-a}{c-a}f(c) \\[1.5ex] &\Leftrightarrow (c-a)f(b) < (c-b)f(a) + (b-a)f(c) \\[1.5ex] &\Leftrightarrow f(a)(b-c) + f(b)(c-a) + f(c)(a-b) < 0 \tag{$*1$} \end{align*}
②가 성립하면 다음과 같이 쓸 수 있다. \begin{align*} \frac{f(b)-f(a)}{b-a} & < \frac{f(c)-f(b)}{c-b} \\[1.5ex] &\Leftrightarrow f(b)(c-b) + f(a)(b-c) < f(c)(b-a) + f(b)(a-b) \tag{$*2$} \end{align*}
$(*1)$과 $(*2)$가 동등함은 쉽게 알 수 있을 것이다. 이것으로써 ① $\Leftrightarrow$ ②가 증명되었다.
① $\Leftrightarrow$ ③과 ① $\Leftrightarrow$ ④는 비슷한 방법으로 증명이 가능하므로 생략한다. $\quad\Box$
정리의 증명 정리의 명제 (1), (2) 중에 후자만 보이도록 하겠다. $(\forall x\in I)(f''(x) > 0)$는 $(\forall a < c \in I)\bigl(f'(a) < f'(c)\bigr)$와 동등하다.
$a < c$일 때 $h>0$가 $a < a + h < c- h < c$가 성립하도록 충분히 작으면, 따름정리의 ③에 의해서 \[ \frac{f(a+h) - f(a)}{h} < \frac{f(c)-f(a)}{c-a} \] 가 성립하며, 따름정리의 ④에 의해서 \[ \frac{f(c)-f(a)}{c-a} < \frac{f(c) - f(c-h)}{h} \] 가 성립한다. $h\rightarrow 0$의 극한을 취하면 $f'(a) = f'(a+) \le f'(c-) = f'(c)$를 얻는다.
부등호 $\le$를 $<$로 바꾸려면 $a < b := \frac{a+c}{2} < c$로 놓고 \[ f'(a) \le \frac{f(b)-f(a)}{b-a} < \frac{f(c)-f(b}{c-b} < f'(c) \tag{*3} \] 를 사용하면 된다. $(*3)$의 부등호는 따름정리의 ②에 의한 것이다. $\quad\Box$
[홈으로]