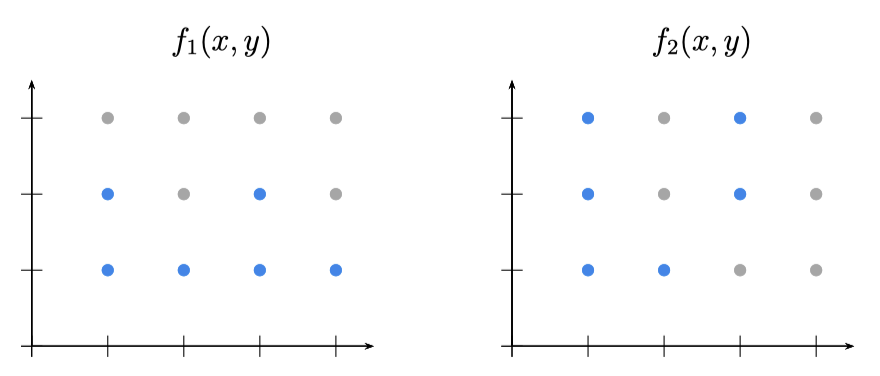
이 문제는 책의 [연습문제 9.12]의 확장 버전으로 생각하면 된다. 다음의 그림에 보인 두 함수 $f_1$과 $f_2$는 정의역이 $\{1,2,3,4\} \times \{1,2,3\}$이고 공역이 $\{0,1\}$이다. 청색 점은 함숫갑 1, 회색 점은 함숫값 0을 뜻한다.

$f_1$의 학습에 있어서, 예측변수를 인코딩 하지 않은 경우, 즉 $x = 1,2,3,4$, $y = 1,2,3$인 경우에는 트레이닝 집합이
xvec_list = to_list(for(x in 1:4) for(y in 1:3) c(x, y)) tvec = c(1,1,0,1,0,0,1,1,0,1,0,0)
가 된다. 예측변수를 2진수로 인코딩 하는 경우에는 xvec_list의 각 원소의 길이는 2가 아닌 4가 될 것이다. 물론 tvec는 변함없이 그대로이다.
$f_2$ 학습의 트레이닝 집합은 $f_1$의 경우와 비교하면 xvec_list은 그대로이고 tvec은 다르다.
문제 1. $f_1$을, 예측변수를 인코딩 하지 않은 경우와 인코딩 하는 경우의 두 방법으로 각각 훈련시킨다. 각 경우에 히든 레이어를 1개만 사용하는 방법과 2개를 사용하는 방법을 각각 사용하여라. 히든 레이어 내의 뉴런의 개수는 3개 이하로 한다.
train_ffnn_wrapper()를 사용하여 신경망을 훈련하고 제대로 되었는지를 확인하여라. 레이어 내의 뉴런의 개수를 변화시켜 가면서 여러 경우들에 걸린 시간을 관찰하고 서술하여라.
문제 2. $f_2$에 대해서도 위와 같은 작업을 하여라. 단, 이때는 히든 레이어를 1개, 2개가 아니라 2개, 3개를 사용해야 한다. 히든 레이어를 3개 사용했을 때는 각 히든 레이어 내의 뉴런의 개수를 5개까지 늘려 보아라.
주의. 반드시 util_ffnn.R을 다운 받아 source()하여 사용한다. util_ffnn.R에 들어 있는 함수는 제출 파일에 있어서는 안 된다.
[홈으로]